domingo, 1 de junio de 2014

VALOR ABSOLUTO DE LA GRAFICA DE UNA FUNCION



En matemática, el valor absoluto o módulo[1] de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.
El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.

Gráfica de la función valor absoluto.

Valor absoluto de un número real

Formalmente, el valor absoluto o módulo de todo número real a\, está definido por:[2]
|a| = \left \{ \begin{array}{rcl} a, & \mbox{si} & a \ge 0 \\ -a, & \mbox{si} & a < 0 \end{array} \right .
Por definición, el valor absoluto de a\, siempre será mayor o igual que cero y nunca negativo.
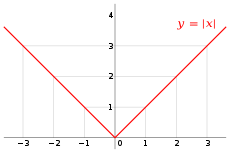
Desde un punto de vista geométrico, el valor absoluto de un número real a\, es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
La función valor absoluto una función continua definida por trozos.

Propiedades fundamentales

|a| \ge 0No negatividad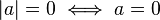
|a| = 0 \iff a = 0Definición positiva
|ab| = |a| |b|\, Propiedad multiplicativa
|a+b| \le |a| + |b|Desigualdad triangular (Véase también Propiedad aditiva)

Otras propiedades

|-a| = |a|\,Simetría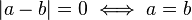
|a-b| = 0 \iff a = bIdentidad de indiscernibles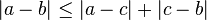
|a-b| \le |a-c| + |c-b|Desigualdad triangular
|a-b| \ge ||a| - |b||(equivalente a la propiedad aditiva)
\left| \frac {a}{b}\right| = \frac {|a|}{|b|} (si \ b \ne 0)Preservación de la división (equivalente a la propiedad multiplicativa)
Otras dos útiles inecuaciones son:
  • |a| \le b \iff -b \le a \le b
  • |a| \ge b \iff a \le -b \vee b \le a
Estas últimas son de gran utilidad para la resolución de inecuaciones, como por ejemplo:
|x-3| \le 9 \iff -9 \le x-3 \le 9
\iff -6 \le x \le 12
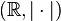El conjunto de los reales con la norma definda por el valor absoluto (\R,|\cdot|) es un espacio de Banach.[cita requerida]

Valor absoluto de un número complejo

El valor absoluto de un número complejo z\, es la distancia r\, desde z\, al origen. Aquí vemos que z\, y su conjugado \bar{z}\, tienen el mismo valor absoluto.

Como los números complejos no conforman un conjunto ordenado en el sentido de los reales, la generalización del concepto no es directa, sino que requiere de la siguiente identidad, que proporciona una definición alternativa y equivalente para el valor absoluto:
|a| = \sqrt{a^2}
De esta manera, dado cualquier número complejo de la forma
z = x + iy\,
con x e y números reales, el valor absoluto o módulo de z está definido formalmente por:
|z| = \sqrt{x^2 + y^2}
Como los números complejos son una generalización de los números reales, es lógico que podamos representar a estos últimos también de esta forma:
|x + i0| = \sqrt{x^2 + 0^2} = \sqrt{x^2} = |x|
De modo similar a la interpretación geométrica del valor absoluto para los números reales, se desprende del Teorema de Pitágoras que el valor absoluto de un número complejo corresponde a la distancia en el plano complejo de ese número hasta el origen, y más en general, que el valor absoluto de la diferencia de dos números complejos es igual a la distancia entre ellos.

Propiedades

El valor absoluto de los complejos comparte todas las propiedades vistas anteriormente para los números reales. Además, si
z = x + i y = r (\cos \phi + i \sin \phi ) \,
y
\bar{z} = x - iy
es el conjugado de z, entonces se verifica que:
|z| = r\,
|z| = |\bar{z}|
|z| = \sqrt{z\bar{z}}
Esta última fórmula es la versión compleja de la primera identidad en los reales que mencionamos en esta sección.
Como los números reales positivos forman un subgrupo de los números complejos bajo el operador de multiplicación, podemos pensar en el valor absoluto como un endomorfismo del grupo multiplicativo de los números complejos.

Programación del valor absoluto

En programación, la función matemática utilizada comúnmente para calcular el valor absoluto es abs(). Esta se utiliza en los lenguajes de programación Fortran, Matlab y GNU Octave (los cuales la soportan para números enteros, reales y complejos), y además en el Lenguaje C, donde también son válidas las funciones labs(), llabs(), fabs(), fabsf() y fabsl().
La codificación de la función valor absoluto para valores enteros es sencilla:
int abs (int i)
{
    if (i < 0)
        return -i;
    else
        return i;
}
Sin embargo, al tratar con puntos flotantes la codificación se complica, pues se debe lidiar con la infinitud y valores NaN.[cita requerida]
Con el lenguaje ensamblador es posible calcular el valor absoluto de un número utilizando sólo tres instrucciones. Por ejemplo, para un registro de 32 bits en una arquitectura x86, con la sintaxis de Intel:

http://youtu.be/Zy2xbX1-Y6E

publicadas por Gerard aguilar @ 10:51 p.m.   0 Comentarios

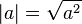
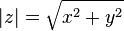
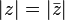
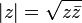
0 Comentarios:

Publicar un comentario

Suscribirse a Comentarios de la entrada [Atom]

<< Página Principal