GRAFICAR FUNCION RAIZ CUADRADA

En lo que sigue, SQRT significa raíz cuadrada. El dominio de la función f definida por f (x) = sqrt (x) es el conjunto de todos los números reales positivos y cero, porque la raíz cuadrada de números negativos no son números reales (pensemos en SQRT (- 4), ¿es real? ). En forma de desigualdad, el dominio de f (x) = sqrt (x) se escribe como x >= 0 en forma de intervalo el dominio está dado por [0, + infinito) Ejemplo 1: Gráfico f (x) = sqrt (x) y encontrar el rango de f. Solución al Ejemplo 1: Debido a que el dominio de f es el conjunto de todos los números reales positivos y cero, se podría construir una tabla de valores de la siguiente manera: x 0 1 4 9 16 Sqrt (x) 0 1 2 3 4 Los valores de x se seleccionaron de modo que la raíz cuadrada de estos valores son números enteros que hacen que sea fácil de trazar los puntos indicados en la tabla. El rango de f está dada por el intervalo [0, + infinito). Ejemplo 2: Gráfico f (x) = sqrt (x - 3) y encontrar el rango de f. Solución al Ejemplo 2: Primero encuentra el dominio de la función raíz cuadrada dado anteriormente al afirmar que la expresión bajo la raíz cuadrada debe ser positivo o igual a cero x - 3 >= 0 Resolver la desigualdad anterior para obtener el dominio de f como el conjunto de todos los valores reales de manera que x >= 3 Ahora seleccione los valores de x en el dominio para construir una tabla de valores. x 3 4 7 12 SQRT (x - 3) 0 1 2. 3 El intervalo [0, + infinito) representa el rango de f. Ejemplo 3: Gráfico f (x) = - SQRT (- 2x + 4) + 1 y encontrar el rango de f. Solución al Ejemplo 3: El dominio de la función dada anteriormente se encuentra mediante el establecimiento de - 2x + 4> = 0 Resolver la desigualdad anterior para obtener el dominio de f como el conjunto de todos los valores reales de manera que x <= 2 Ahora seleccione los valores de x en el dominio de f para construir una tabla de valores. Estos valores son seleccionados de manera que la raíz cuadrada plazo es un número entero y dar puntos que son fáciles de trazar. x 2. 3 / 2 0 -5 / 2 -6 - SQRT (-2 x + 4) + 1 1 0 -1 -2 3- El rango de f está dada por el intervalo (-infinito, 1]. Ejemplo 4: Gráfico f (x) = sqrt (- x 2 + 4) y encontrar el rango de f. Solución del Ejemplo 4: El dominio de la función dada anteriormente se encuentra resolviendo el polinomio de la desigualdad - x 2 + 4 >= 0 La solución de conjunto de la desigualdad anterior está dado por el intervalo de [-2, 2] que es también el dominio de la función anterior. Escribamos la función dada como una ecuación de la siguiente manera y = SQRT (- x 2 + 4) Plaza de ambas partes y hacer arreglos para obtener. x 2 + y 2 = 2 2 Ejemplo 5: Gráfico f (x) = sqrt (x 2 - 9) y encontrar el rango de f. Solución del Ejemplo 5: El dominio de la función dada anteriormente se encuentra por la solución de x 2 - 9 >= 0 Lo que da un dominio por reprsented (-infinito, -3] U [3, + infinito) Ahora seleccione los valores de x en el dominio de f para construir una tabla de valores, tomando nota de f (x) = f (-x) por lo tanto, una simetría de la gráfica con respecto al eje y. 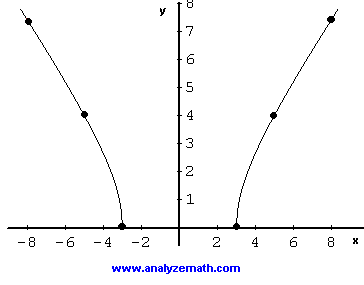x 3 5 8 SQRT (x 2 - 9) 0 4 7,4 El rango de f está dada por el intervalo [0, + infinito). Ejemplo 6: Gráfico f (x) = sqrt (x 2 - 6x + 9) y encontrar el rango de f. Solución al Ejemplo 6: Usemos escribir la expresión en la raíz cuadrada de un cuadrado de la siguiente manera x 2 - 6x + 9 = (x - 3) 2 Por lo tanto f (x) = sqrt (x 2 - 6x + 9) = SQRT ((x - 3) 2) = | x - 3 | La función dada ha sido rewitten como una función de valor absoluto. La función f se puede escribir como una función a trozos y graficarse de la siguiente manera. El rango de f está dada por el intervalo [0, + infinito). Ejemplo 7: Gráfico f (x) = sqrt (x 2 + 4x + 6) y encontrar el rango de f. Solución del Ejemplo 7: Uso de completar el cuadrado para rewtite la expresión bajo la raíz cuadrada de la siguiente manera x 2 + 4x + 6 = (x + 2) 2 + 2 La expresión bajo la raíz cuadrada es siempre positiva por lo tanto, el dominio de f es el conjunto de todos los números reales. Veamos primero en la gráfica de (x + 2) 2 + 2. Es una parábola. Es de esperar que la gráfica de f para tener el mismo eje de simetría, la línea vertical, x = -2 como el gráfico de arriba. La tabla de valores puede construirse de la siguiente manera. 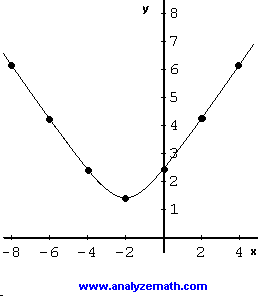x 2 0 2 4 SQRT ((x + 2) 2 + 2) 1,4 2,4 4,2 6,2 El rango de f está dada por el intervalo [sqrt (2), + infinito

http://youtu.be/8WyyR-wx9lA