Administracion de empresas

martes, 3 de junio de 2014

DERIVADA DE FUNCION POR DEFINICION

La función derivada de una función f(x) es una función que asocia a cada número real su derivada, si existe. Se expresa por f'(x).

Ejemplos

Determinar la función derivada de f(x) = x² − x + 1.

Calcular f'(−1), f'(0) y f'(1)

f'(−1) = 2(−1) − 1 = −3

f'(0) = 2(0) − 1 = −1

f'(1) = 2(1) − 1 = 1

Derivada de las funciones a trozos

En las funciones definidas a trozos es necesario estudiar las derivadas laterales en los puntos de separación de los distintos trozos.

Estudiar la derivabilidad de la función f(x) = |x|.

Puesto que las derivadas laterales en x = 0 son distintas, la función no es derivable en dicho punto.

Las derivada laterales no coinciden en los picos ni en los puntos angulosos de las funciones. Por tanto en esos puntos no existe la derivada.

No es derivable en x = 0.

Hallar el punto en que y = |x + 2| no tiene derivada. Justificar el resultado representando su gráfica.

La función es continua en toda

f'(−2)⁻ = −1f'(−2)⁺ = 1

No será derivable en: x= -2.

En x = -2 hay un pico, por lo que no es derivable en x= -2.

Hallar los puntos en que y = |x ² − 5x + 6| no tiene derivada. Justificar el resultado representando su gráfica.

La función es continua en toda

f'(2)^- = −1f'(2)⁺ = 1

f'(3)^- = −1f'(3)⁺ = 1

Como no coinciden las derivadas laterales la función no será derivable en: x=2 y x=3.

Podemos observar que en x = 2 y en x = 3 tenemos dos puntos angulosos, por lo que la función no será derivable en ellos.

https://www.youtube.com/watch?v=BvQaykh5Si4

FUNCIONES

En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r². Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.

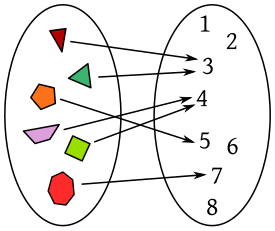
En análisis matemático, el concepto general de función, aplicación o mapeo se refiere en a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero):

...	−2 → +4,	−1 → +1,	±0 → ±0,
	+1 → +1,	+2 → +4,	+3 → +9,	...

Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. Aunque las funciones que manipulan números son las más conocidas, no son el único ejemplo: puede imaginarse una función que a cada palabra del español le asigne su letra inicial:

...,

Estación → E,

Museo → M,

Arroyo → A,

Rosa → R,

Avión → A,

...

Esta es una función entre el conjunto de las palabras del español y el conjunto de las letras del alfabeto español.

La manera habitual de denotar una función f es:

f: A → B

a → f(a),

donde A es el dominio de la función f, su primer conjunto o conjunto de partida; y B es el codominio de f, su segundo conjunto o conjunto de llegada. Por f(a) se denota la regla o algoritmo para obtener la imagen de un cierto objeto arbitrario a del dominio A, es decir, el (único) objeto de B que le corresponde. En ocasiones esta expresión es suficiente para especificar la función por completo, infiriendo el dominio y codominio por el contexto. En el ejemplo anterior, las funciones «cuadrado» e «inicial», llámeseles f y g, se denotarían entonces como:

f: Z → N

k → k², o sencillamente f(k) = k²;

g: V → A

p → Inicial de p;

si se conviene V = {Palabras del español} y A = {Alfabeto español}.

Una función puede representarse de diversas formas: mediante el citado algoritmo o ecuaciones para obtener la imagen de cada elemento, mediante una tabla de valores que empareje cada valor de la variable independiente con su imagen —como las mostradas arriba—, o como una gráfica que dé una imagen de la función.

El concepto de función como un objeto matemático independiente, susceptible de ser estudiado por sí solo, no apareció hasta los inicios del cálculo en el siglo XVII.^[1] René Descartes, Isaac Newton y Gottfried Leibniz establecieron la idea de función como dependencia entre dos cantidades variables. Leibniz en particular acuñó los términos «función», «variable», «constante» y «parámetro». La notación f(x) fue utilizada por primera vez por A.C. Clairaut, y por Leonhard Euler en su obra Commentarii de San petersburgo en 1736.^[2] ^[3] ^[4]

Inicialmente, una función se identificaba a efectos prácticos con una expresión analítica que permitía calcular sus valores. Sin embargo, esta definición tenía algunas limitaciones: expresiones distintas pueden arrojar los mismos valores, y no todas las «dependencias» entre dos cantidades pueden expresarse de esta manera. En 1837 Dirichlet propuso la definición moderna de función numérica como una correspondencia cualquiera entre dos conjuntos de números, que asocia a cada número en el primer conjunto un único número del segundo.

La intuición sobre el concepto de función también evolucionó. Inicialmente la dependencia entre dos cantidades se imaginaba como un proceso físico, de modo que su expresión algebraica capturaba la ley física que correspondía a este. La tendencia a una mayor abstracción se vio reforzada a medida que se encontraron ejemplos de funciones sin expresión analítica o representación geométrica sencillas, o sin relación con ningún fenómeno natural; y por los ejemplos «patológicos» como funciones continuas sin derivada en ningún punto.

Durante el siglo XIX Julius Wilhelm Richard Dedekind, Karl Weierstrass, Georg Cantor, partiendo de un estudio profundo de los números reales, desarrollaron la teoría de funciones, siendo esta teoría independiente del sistema de numeración empleado.^{[cita requerida]} Con el desarrollo de la teoría de conjuntos, en los siglos XIX y XX surgió la definición actual de función, como una correspondencia entre dos conjuntos de objetos cualesquiera, no necesariamente numéricos.^[5] También se asoció con otros conceptos vinculados como el de relación binaria

https://www.youtube.com/watch?v=oo-OlMQI7nI

http://es.wikipedia.org/wiki/Funci%C3%B3n_matem%C3%A1tica

FUNCIONES ESPECIALES

Una función especial es una función matemática particular, que por su importancia en el campo del análisis matemático, análisis funcional, la física y otras aplicaciones, posee nombres y designaciones más o menos establecidos.

No existe una definición general de las mismas, pero la lista de funciones matemáticas contiene funciones que son generalmente aceptadas como especiales. En particular, las funciones elementales son también consideradas funciones especiales.

Muchas funciones especiales se originan como soluciones a ecuaciones diferenciales o integrales de funciones elementales. Por lo tanto, las tablas de integrales ^[1] por lo general incluyen la descripción de algunas funciones especiales, y las tablas de funciones especiales ^[2] incluyen las integrales más importantes; por lo menos, la representación integral de las funciones especiales.

Lenguajes computacionales de cálculo analítico tales como Mathematica^[3] por lo general reconocen a la mayoría de las funciones especiales. Sin embargo, no todos los sistemas de cálculo poseen algoritmos eficientes de evaluación, especialmente en el plano complejo.